Introduction

clustering demo

Clustering a unique problem which falls under the category of unsupervised machine learning system. In neural networks it also is a type of classification problem, which separates the inputs into different classes.

As there is no training set available to hint or teach the system as to which point belongs to which class, this is an unsupervised learning. Only thing known to the system is how many clusters it requires to form (the k). The number of clusters can also be computed using stochastic / heuristics of initial analysis of the inputs. It is one of the simpler clustering problems. There are more advanced clustering ways like Linear Vector Quantisation (LVQs) and Self-organising maps (SOMs).

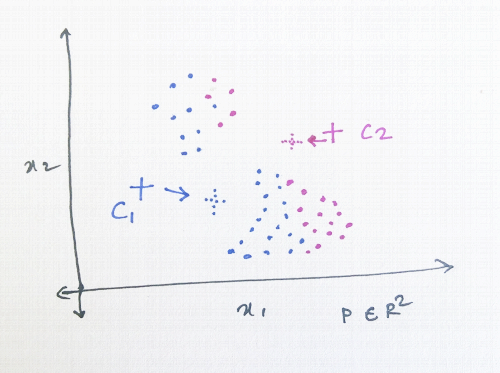
It works well when the problem is more intuitive i.e. if we can visualise different clusters as there is a good amount of separation between them (example Fig. a). It is also useful when the problem space is intermixed (example Fig. b) yet we would like to divide the space into certain clusters.

clustering

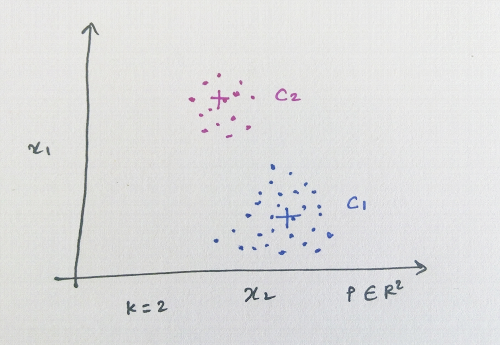
Fig a

clustering closely spaced inputs

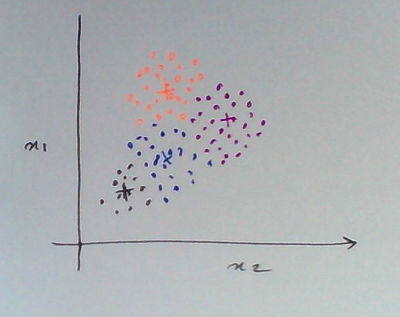
Fig b

Clustering is a NP hard problem. k-Means is more of a heuristic algorithm, which is trying to solve this NP hard problem. This algorithm is not able to find the global minima, it converges onto a local minima. As you can try for yourself in the below implementation of the k-Means. The quality of the solution is dependent on the location of the initial guess of the centroids.

The Algorithm

Inputs

P = Set of input points where every point in P is belonging to space of n dimensions.

k = number of clusters

The algorithm will try to minimise the following function

minimization function

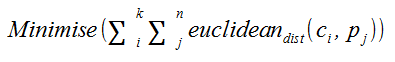
Step 1

This is an unsupervised learning, hence we start with the analysis of input data and keep adapting our computations based on new data. Take the available input data

clustering input

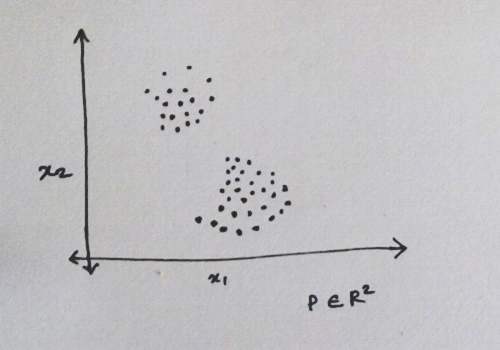
Step 2

Initialise the k cluster points in the input space. This initialisation is important as this alogrithm will latch onto a local minima. We are going to take random point in the bounding box of the inputs.

Step 3

Compute the distances of each point in the input space to the cluster points.

clustering stage 1

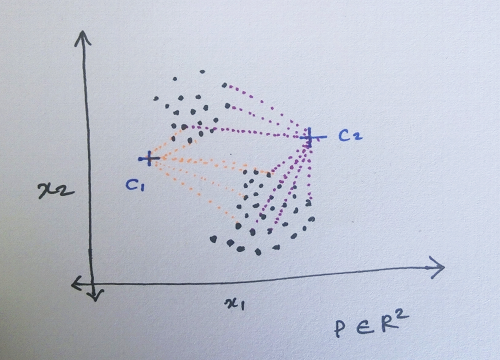
Step 4

Associate each point to the cluster point which is the nearest to it using the distances computed. You can combine step 3 and 4 for optimisation.

clustering stage 2

Step 5

Compute a centroid of the points associated with the each cluster. So there will be k new centroids. Move the cluster points to the new centroid positions.

Refer above fig.

Step 6

If there is any change in the cluster position, repeat step 3 to 5.

To achieve global minima one can use the stochastic techniques or search techniques like Simulated Annealing.

Interactive js example


Enter the number of clusters


These cluster centroids are then used to compute a voronoi region. More to come in the later posts.